Um algoritmo guloso pode ser utilizado para resolver problemas que não possuem um algoritmo que resolveria de forma rápida.
Esse algoritmo, em cada iteração, irá fazer a escolha que parece ser a melhor no momento para chegar na melhor solução final que ele consegue.
Implementação
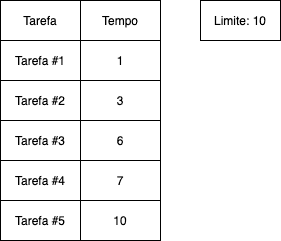
Um exemplo básico, você possui um tempo limite para completar uma série de tarefas e cada tarefa possui um tempo para ser completada.
Esse é um problema que um algoritmo guloso pode resolver. Você precisa escolher o máximo de tarefas que consegue completar dentro desse limite.
tasks = [1, 3, 6, 7, 10]
max_time = 10
current_time = 0
current_tasks = 0
for task_time in tasks:
current_time += task_time
if current_time > max_time:
break
current_tasks += 1Veja que a lista de tarefas está ordenada e a cada iteração o algoritmo irá adicionar o tempo da tarefa task_time ao tempo atual current_time e fazer uma verificação, caso o tempo não tenha atingido o limite, o algoritmo irá incrementar o número de tarefas para fazer current_tasks, caso contrário o loop é encerrado.
Esse algoritmo em nenhum momento volta atrás de uma decisão, ele apenas escolhe a tarefa pensando que ela é a ideal para o momento.
E a resposta final desse algoritmo é 3 tarefas.
Algoritmo de Dijkstra
O algoritmo de Dijkstra também é um ótimo exemplo de um algoritmo guloso, ele é usado para calcular o caminho mínimo entre um vértice inicial e todos os outros vértices em um grafo com pesos não negativos.
Esse algoritmo é considerado guloso pois a cada iteração ele irá tentar fazer o movimento que tem o menor peso de acordo com as possibilidades atuais e o algoritmo nunca voltará atrás de uma decisão que ele tenha feito.
Implementação
Vou utilizar apenas algumas partes do código para explicar, mas o código completo você pode ver aqui: dijkstra.py
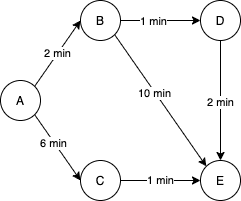
Para inicializar, precisamos definir os vértices e os pesos das arestas do nosso grafo.
Essa é a representação do diagrama mostrado acima:
graph = Graph()
# Vértices
graph.add_node('a')
graph.add_node('b')
graph.add_node('c')
graph.add_node('d')
graph.add_node('e')
# Arestas com os pesos
graph.add_edge('a', 'b', 2)
graph.add_edge('a', 'c', 6)
graph.add_edge('b', 'd', 1)
graph.add_edge('b', 'e', 10)
graph.add_edge('c', 'e', 1)
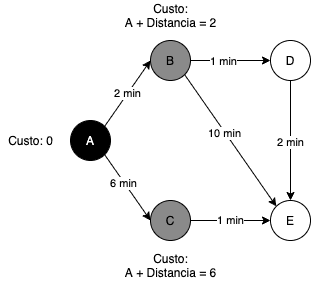
graph.add_edge('d', 'e', 2)O primeiro passo do algoritmo é definir o ponto inicial e nesse caso vai ser o A e como este ponto é o início, ele vai ter custo 0 pois para chegar até ele não existe nenhum outro passo. Já os outros vértices receberão o custo como infinito pois como não sabemos ainda como chegar neles precisamos definir o maior custo possível.
O algoritmo então irá procurar o vértice que tenha o menor custo e que ainda não foi visitado. Todos os outros vértices possuem o custo definido como infinito, então o que terá o menor custo será o vértice A e esse é o ponto inicial do algoritmo.
Para cada movimento a partir de A, o algoritmo irá atualizar os custos para se chegar até eles, somando o custo de A que é 0 com o peso da distância, se essa soma for menor que o custo atual do vértice, então esse valor será atualizado. Lembrando que definimos todos os vértices com o custo infinito.
# Busca o menor vértice ainda não visitado
node = graph.find_lowest_cost_node()
while node:
# Recupera o custo desse vértice
cost = graph.costs.get(node)
# Recupera todas as arestas do vértice
edges = graph.edges.get(node) if graph.edges.get(node) else []
for edge in edges:
distance = graph.distances.get((node, edge))
new_cost = cost + distance
current_edge_cost = graph.costs.get(edge)
# Para cada aresta, realiza a soma do custo com a distância
# E caso essa soma for menor que o custo atual, atualize o custo
if new_cost < current_edge_cost:
graph.update_node_cost(edge, new_cost)
graph.update_node_parent(edge, node)
# Marca o vértice como visitado
graph.visit_node(node)
# Busca o menor vértice ainda não visitado e continua o loop
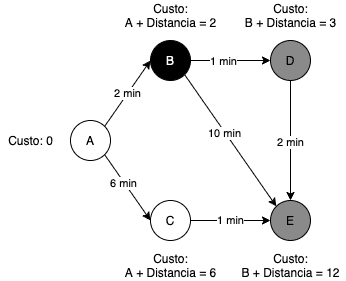
node = graph.find_lowest_cost_node()O algoritmo marca o A como visitado e começa a iteração novamente, procurando o próximo vértice não visitado com o menor peso.
Nesse caso será o B e ele irá fazer os mesmos cálculos mostrados acima.
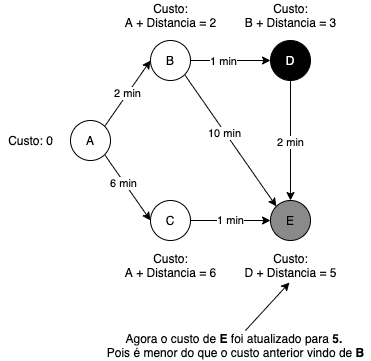
Agora para D:
O vértice E é o próximo, mas não possui nenhuma aresta, então o algoritmo irá apenas marcar como visitado.
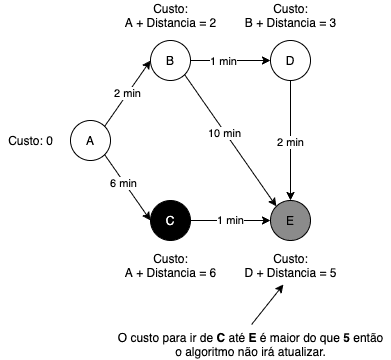
Por último o algoritmo passa por C.
Note que C tem caminho para ir até E, porém ele não atualiza o custo pois é maior do que o custo atual em E:
O resultado final é:
a -> b -> d -> eE esse é o melhor caminho para E iniciando em A. Com o custo total de 5.
O código completo você pode ver aqui: dijkstra.py
Algoritmo de Bellman-Ford
Para grafos ponderados e com pesos negativos o algoritmo de Dijkstra não irá funcionar, porém existe o Algoritmo de Bellman-Ford que pode ser utilizado para isso.